DeepSeek just released a “math prodigy”—and it matters
This week, DeepSeek quietly dropped a new model: DeepSeekMath-V2. It’s not a general-purpose chatbot designed for casual conversations. It’s a model optimized for natural-language theorem proving—demonstrating what the team calls “self-verifiable mathematical reasoning.” And by every measure available, it’s rewriting expectations for what open models can do in a narrow, demanding domain.
On Putnam 2024—a notoriously difficult undergraduate math competition where the highest human score was 90—DeepSeekMath-V2 posted 118 out of 120. On the International Mathematical Olympiad (IMO 2025) and China Mathematical Olympiad (CMO 2024), it achieved gold-medal-level performance.
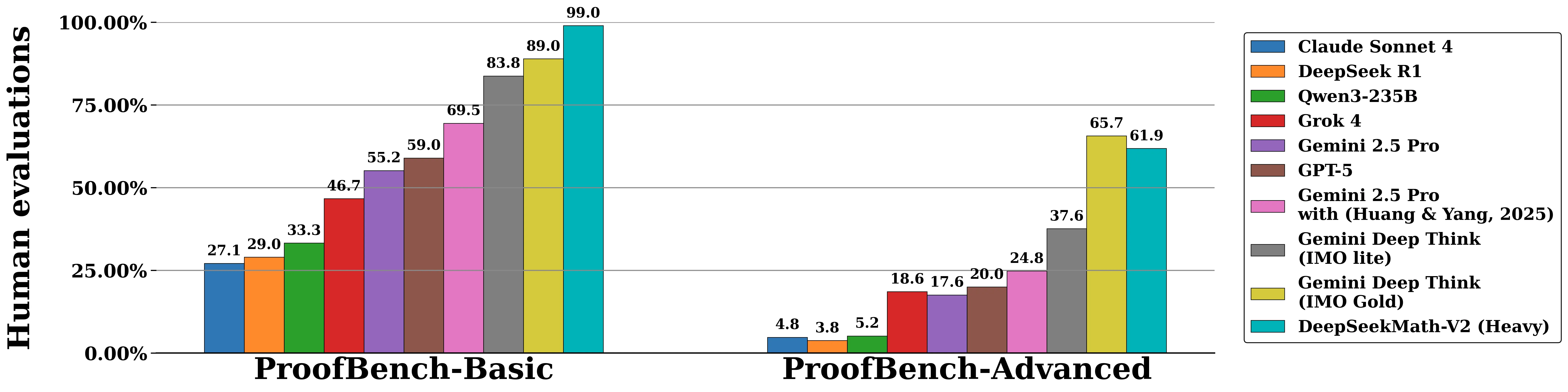
On the IMO-ProofBench benchmark (developed by DeepMind), DeepSeekMath-V2 outperformed DeepMind’s DeepThink (IMO Gold) on the Basic set and remained competitive on the Advanced set, substantially outperforming all other baselines including GPT-5, Gemini 2.5 Pro, and Claude Sonnet 4.
Why math competition results matter more than you think
These competitions are nothing like standardized tests. Getting the right answer isn’t enough. Contestants must produce complete, rigorous, logically self-consistent proofs. Any visible gap in reasoning—any significant leap without justification—can tank your score to near zero, even if the final answer is correct.
The conventional approach to RL for mathematical reasoning—rewarding models based on whether final answers match ground truth—has two fundamental limitations. First, correct answers don’t guarantee correct reasoning; a model can arrive at the right answer through flawed logic. Second, this approach doesn’t work for theorem proving, where rigorous derivation is the primary objective.
So when we say “IMO gold” plus “118/120 on Putnam,” we’re not just talking about stronger compute. We’re talking about genuine progress on:
- Long-chain reasoning: holding coherent logic across many steps.
- Rigorous construction: building proofs that withstand scrutiny.
- Hallucination resistance: not inventing plausible-sounding but wrong steps.
This isn’t next-token prediction dressed up in a lab coat. It’s something closer to actual thinking.
The engine: self-verifiable mathematical reasoning
DeepSeek didn’t keep its approach locked away. They’ve published the core architecture—a system built around proof verification and self-verification. Think of it as a rigorous academic review process built into the training loop.
Component 1: The Proof Verifier
Traditional models focus on outputs. DeepSeek trained a dedicated verifier to evaluate proofs using a three-level scoring system: 1 for complete and rigorous proofs, 0.5 for proofs with sound logic but minor errors, and 0 for fundamentally flawed proofs. The verifier doesn’t just check final answers—it examines whether each reasoning step is properly justified.
Component 2: Meta-Verification
Here’s the clever part. The verifier is still a model—and models hallucinate. When evaluating flawed proofs, a verifier might claim to find issues that don’t actually exist, receiving full reward for predicting the correct score while fabricating non-existent problems.
To fix this, DeepSeek introduced meta-verification: a secondary evaluation that checks whether the issues identified by the verifier actually exist and whether the verifier’s reasoning is sound. This dramatically reduces hallucinated errors—the meta-verifier improved verifier quality scores from 0.85 to 0.96.
Component 3: Self-Verifying Generator
With feedback from both layers, the proof generator learns to evaluate its own work. During training, the model produces a proof followed by a self-analysis using the same rubrics as the verifier. The reward structure is key: honestly admitting mistakes earns higher reward than falsely claiming correctness.
This creates a powerful incentive: the best strategy for high rewards is to identify and resolve as many issues as possible before finalizing the proof.
The synergy that makes it work
The verifier and generator create a virtuous cycle:
- The verifier improves the generator by providing accurate feedback.
- As the generator improves, it produces harder-to-verify proofs that challenge the verifier.
- These challenging cases become training data to improve the verifier.
- Scaled verification compute can automatically label new proofs without human annotation.
For the hardest problems, DeepSeek scales both verification and generation compute—using extensive verification to catch subtle issues and parallel generation to explore diverse proof strategies. Problems not fully solved typically have their genuine issues correctly identified by the generator, while fully solved problems pass all verification attempts.
What this means—and where it doesn’t apply yet
Self-verification shines when “correct” and “incorrect” are well-defined. Math proofs, formal logic, and code have that property. In subjective domains—literary style, open-ended creativity—the grading criteria blur, and the approach loses traction. Generalization there remains an open problem.
But for structured, high-stakes reasoning tasks, the lesson is clear: within the existing LLM paradigm, clever verification mechanisms can push specialized performance to—or beyond—top human levels. No new fundamental architecture required; just a better feedback loop.
Why this matters for the rest of us
DeepSeekMath-V2 isn’t a product most developers will call directly. But it signals something bigger:
- Open-source models can compete on hard reasoning benchmarks, not just chat fluency.
- Self-verification as a training objective may be a repeatable playbook—applicable to code review, formal methods, and beyond.
- Rewarding honesty over confidence could shape how we build reliable AI tools that don’t confidently lie to you.
The key technical insight: you can train LLM-based verifiers to assess proofs that were previously considered too hard to verify automatically. By scaling test-time compute under verifier guidance, the model solves problems that require hours of effort from human competitors.
As the paper notes: “This work establishes that LLMs can develop meaningful self-evaluation abilities for complex reasoning tasks.” If you care about AI safety, interpretability, or just building systems you can trust, this architecture deserves attention.